
Trsper: a web-based application for Archimedes spiral analysis
Introduction
Archimedes spiral drawing is a cornerstone of the movement disorders exam. Clinically validated, automatic analysis metrics have been developed, including: frequency (1-4) and spiral axis in essential tremor (ET) (5) and simulated dystonic tremor (6); loop width variation in ET (7), Niemann-Pick disease type C (8), Parkinson’s disease (9), multiple sclerosis, and functional tremor (10); and velocity (11,12). Studies investigating these metrics have digitized the spiral exam through scanned paper drawings (13-15) or Wacom tablet applications, which capture pen strokes from a pen-and-paper drawing (2,3,16-18). NeuroGlyphics (2) (http://neuroglyphics.org/) and MovAlyzeR (http://neuroscript.net/) are example Wacom programs. Other applications for personal digital assistants (19-21), iPad (22), and mobile phone have been developed (23). The effects of drawing instructions on outcomes, e.g., comparing tracing a template to drawing freehand, have also been explored (24). Notably, the group found that different drawing instructions affected ratings of spiral severity.
To increase access to a digital exam format, we built a web-based platform for mobile touchscreen devices that incorporates clinically validated metrics, such as 1st and 2nd order smoothness (25). Then, we assessed in-application characterization of spirals drawn by healthy volunteers following varying instruction sets (24) and compared consistency across instruction sets and individuals. Our analysis reveals that instruction set and drawing implement affect spiral metrics. These experiments introduce a tool and set of instructions for its use that may afford greater sensitivity and specificity for detection of pathology through Archimedes spiral drawing. In addition, as our web-based platform can be accessed freely, remotely, and without the requirement for any specialized equipment beyond consumer grade tablets or smart phones, it also has the advantage of lowering economic and physical barriers to testing. Future validation experiments will evaluate the application’s performance in identification of abnormal movements in diverse patient populations (e.g., those with dystonia, tremor, myoclonus) and help us to amend and expand the tool to better characterize those abnormalities. Further experiments will also expand our understanding of how well the application tracks changes in movements caused by disease progression or by normal aging. We present the following article in accordance with the MDAR reporting checklist (available at https://dx.doi.org/10.21037/mhealth-21-16).
Methods
Web application design
The web application for Archimedes spiral analysis was written using HTML5 and vanilla Javascript code (http://www.trsper.com) (Figure 1). The website will remain freely available, and the code is open source and available for download. For the background spiral, simulated ideal Archimedean spiral Cartesian coordinates are calculated according to the formula: x = (vt + c)cos wt, y = (vt + c)sin wt, where t represents time and w and v are constants reflecting the angular velocity of the spiral’s rotation about the origin. Users draw in the main canvas and all touch points are stored locally as x, y coordinates and time, then drawn as a blue line with a refresh rate of 50 Hz.

Participants
Volunteers were recruited through emails to Thomas Jefferson University students. All volunteers were putatively healthy, equally distributed by gender (task one: 4 female, 6 male; task two: 6 female, 4 male), and spanned ages 28 to 55. All participants were informed of the purpose of the study and consented for participation. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The Thomas Jefferson University Institutional Review Board reviewed and exempted the study (Control #20E.990).
Spiral drawing tasks
Ten distinct volunteers each were recruited for two separate tasks. In one (Figure 2), volunteers drew five spirals each according to six previously described instruction sets (24) (n=30 per person). They used a passive stylus and an iPad. Briefly, instructions were: tracing—trace the background spiral, non-tracing—draw between the lines of it, or draw freehand, while either resting their drawing arm/hand comfortably on the table or lifting it and allowing no contact between their entire arm and the table. When drawing “freehand”, users were asked to recreate the size and shape of the background spiral that they previously saw to the best of their ability. We then analyzed each spiral according to the metrics described below in order to determine how the instructions affected the consistency of drawn spirals (Figure 3). In task two (Figure 4), volunteers drew five spirals each using both a passive stylus and their dominant index finger, according to the two most consistent instruction sets as determined in task one (Figure 3D).
Spiral metrics
Spiral metrics were adapted from prior publications and included:
-
for i =0 to N (3)
-
for i =0 to N (3)
-
for i =0 to N (3)
-
for i =0 to N (3)
-
or the average coefficient of variation of given spiral widths through all angles 0 to 360 (7)
-
(25)
-
(25)
-
(25)
-
(25)
Simulated spirals and decision support
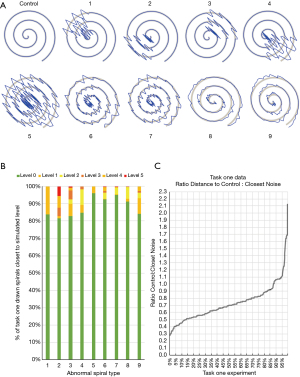
To build decision support, we simulated “abnormal” spirals by first calculating an ideal Archimedes spiral, dithering every point by 4 pixels in either x or y direction with 50% probability, and then adding noise from an ideal cosine function to create 9 distinct spiral types 1 through 9 (Figure 5A). For types 1 through 4, cosine noise was added to only 1 of the 4 spiral quadrants. For type 5, cosine noise was added to all 4 quadrants which was then doubled and changed every 5 points to generate types 6 and 7. Similarly, types 8 and 9 were generated using the same method as types 6 and 7, but only half the amount of cosine noise was added to each quadrant.
We simulated each of the 10 spiral types 2,000 times, at each of 20 possible sizes. We then found the centroid (Figure S1A) of each of the 2,000 simulations, resulting in 200 total centroids. Next, we calculated the distance between the drawn spiral and the control or type 0 spiral for each of the 20 possible sizes, as well as the closest centroid for the 9 types of abnormal spirals in that size. Finally, we calculate a ratio of these distances for each of the 20 possible sizes. We then report the 5 ratios closest to the size of the drawn spiral, by comparing the area of the drawn spiral (calculated using x and y bounds of the spiral) to each of the 20 possible sizes we simulated.
Statistical analysis
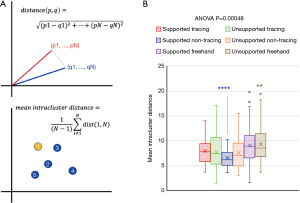
All spiral coordinates were first transformed from Cartesian to polar coordinates, following the formulae: and where theta was computed in radians and the values adjusted so they continuously increased from zero, as previously described (25). We represented each individual experiment as an n-dimensional vector of spiral metrics. Principal components analysis (PCA) transformed high-dimensional data into lower dimensions that preserved variability and allowed for visualization of relationships across conditions. K-means clustering quantified relative relationships of PCA groups. For each group of 5 technical replicates, we then calculated the distance between an experiment and each of the 4 other members of its group using Euclidean distance: (Figure 2A). We used ANOVA and one-vs.-all t-tests to compare this calculated metric in our experiments. All original data were included in the study. All data were normally distributed according to a Kolmogorov-Smirnov test.
Results
To validate our spiral drawing application (Figure 1), we tested the effect of distinct drawing instructions that practicing neurologists might give patients (see Methods).
PCA
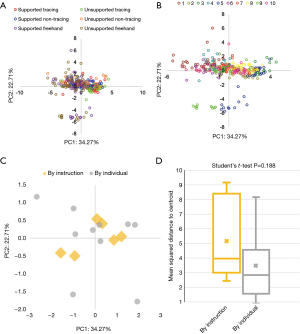
We visualized our data using PCA, which reduces data dimensions while preserving variability. PCA of task one data with all 11 metrics and coloring by instruction set reveals outliers in each freehand instruction set (Figure 2A), as well as clustering by instruction set. Coloring observations by subject rather than by instruction set also reveals outliers (Figure 2B) and clustering by subject.
K-means clustering to determine the center of each of these clusters (Figure 2C) in the PCA transformation reveals a significant increase in the distance between centers, comparing six instruction sets (mean =1.441) to the ten subjects (mean =2.213) (Student’s t-test P value =0.006). The mean squared distance of points to the cluster centroid is higher when clustering by the six instruction sets (mean =5.141) as compared to clustering by the ten subjects (mean =3.463), although this difference is not statistically significant (Student’s t-test P value =0.188) (Figure 2D). These results suggest there was more variation in the 11 calculated metrics between subjects than between instructions.
Intracluster distance by instruction set and individual
We next investigated the effect of drawing instructions on the consistency of spiral metrics from each individual, by calculating the mean Euclidean distance (Figure 3A) between each replicate (represented as 11-dimensional vectors of spiral metrics) and the other 4 replicates in their experimental group (dubbed “mean intracluster distance”). The mean Euclidean intracluster distance differed significantly across the six instruction sets (ANOVA P value =4.8×10−4; Figure 3B), similarly to observer-rated tremor severity in a prior study of the effect of drawing instructions on hand-drawn spirals. Notably, supported non-tracing differed significantly from all other groups (one-vs.-all Student’s t-test P value <0.0001; Figure 3B), as did unsupported freehand (one-vs.-all Student’s t-test P value <0.005; Figure 3B). As a result, we concluded that the supported non-tracing instruction set produces drawings with the most consistent spiral metrics, while the unsupported freehand instruction set produces drawings with the least consistent spiral metrics.
Intracluster and intercluster distance of finger or stylus drawn spirals
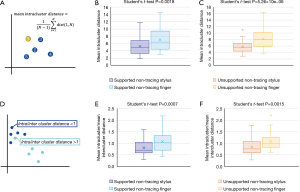
For task two (Figure 4), we examined the effects of drawing with a stylus as compared to drawing with a finger. For comparison, we calculated the ratio of mean intracluster over mean intercluster distance (Figure 4D), where a ratio >1 indicates a point that is closer to the points in the opposite group, while a ratio <1 indicates a point that is closer to points within the same group.
When comparing stylus drawings to finger drawings individually in each instruction set, we found lower mean intracluster distances (Figure 4A) for stylus drawn spirals in both the supported non-tracing (mean 5.21 vs. 6.99; Student’s t-test P value =0.0018; Figure 4B) and unsupported non-tracing (5.72 vs. 8.09; Student’s t-test P value =5.26×10−6; Figure 4C) instruction sets, suggesting stylus drawn spirals are more consistent than finger drawn spirals in these instruction sets. Consistent with these results, we also found lower mean ratios of mean intra/inter-cluster distances (Figure 4D) in stylus drawings for both supported non-tracing (0.81 vs. 1.08; Student’s t-test P value =0.0007; Figure 4E) and unsupported non-tracing (0.84 vs. 1.09; Student’s t-test P value =0.0015; Figure 4F). Together, these results suggest that drawing with a stylus produced more consistent spirals than drawing with the dominant index finger.
Decision support
We next tried to determine whether we could generate abnormal spirals mathematically by introducing tremulous artefacts into simulated spiral drawings. We first simulated control spirals and then simulated 9 different types of abnormal spiral (Figure 5A). For each of the 9 types, we simulated n=2,000 spirals at 6 different “levels”, with level 0 being a control or normal spiral and each subsequent level combining a higher amplitude of abnormal spiral with the control template. To assess whether our abnormal simulated spirals differed substantially from drawn control spirals, we calculated the distance between all drawn spirals in task 1 and the centroids of both the abnormal simulated spirals and control spirals. Using these distances, we classified each drawn spiral as either being closer to the control spiral or one of five levels of simulated abnormal spirals. As one example, 84% of drawn spirals were closer to control than any of the levels of the type 1 spiral (Figure 5B). As expected, most drawn spirals clustered with the control type spirals, regardless of simulated spiral type (Figure 5B). Thus, our mathematically simulated abnormal spirals can be accurately differentiated from spirals drawn by healthy volunteers.
To determine the appropriate number of simulations for use in a decision support system, we then simulated ten groups of control ideal Archimedean spirals with n=10, 50, 100, 250, 500, 750, 1,000, 2,000, 5,000, and 10,000. To analyze each individual spirals against each other, we computed centroids (Figure S1A) based on PCA. We calculated spiral metrics for these 10 groups and plotted both a PCA (Figure S1B), as well as distance to the PCA centroid (Figure S1C). Of note, distance to the centroid plateaued above n=2,000 simulations, indicating that additional spiral simulations did not contribute new information.
Finally, we calculated the ratio of distance to “control” simulation over distance to the nearest abnormal spiral of any of 9 types, for all 300 spirals from task one and for all sizes of simulated spiral (n=20). We then plot the minima for all 300 drawn spirals in ascending order, with range 0.28 to 2.73 (Figure 5C). Ninety-five percent of all drawn spirals showed ratio <1.1, indicating that the majority of drawn spirals were closer to control simulation than the most comparable abnormal simulation. Thus, we take all values >1.1 to be considered “abnormal” in our decision support system.
Discussion
We developed a web-based, touchscreen application for the Archimedes spiral drawing task that implements validated metrics for spiral analysis. We then conducted experiments with healthy volunteers to determine the application’s discriminatory capacity. We analyzed a potential workflow using this application into our experiments, asking volunteers to follow six different published instruction sets—task one, and to draw with a stylus or their dominant index finger—task two. Analysis of data from task one suggested that more variability between the individual experiments is explained by individual subject rather than instruction set used. In turn, these observations suggest that these metrics capture true biological variability, because the metrics were more sensitive to who was drawing the spirals than how they drew them.
Assessing the instruction sets using Euclidean distance showed that supported non-tracing drawings and unsupported freehand drawings produced the most and least consistent replicates, respectively. Prior work with these instruction sets found that supported drawings were rated less severely than unsupported drawings, but showed lower intra- and inter-rater reliability (24). Due to the inherent difference in these tasks with regard to comfort and sensory cues, this result is biologically sound and supports our hypothesis that drawing task affects spiral consistency. We reason that these results may affect sensitivity and specificity of clinically validated metrics like spiral width variability (7,10) as they capture disease correlates. As drawing unsupported and freehand strips away visual and physical compensations for tremor, these instruction sets may be the most sensitive for capturing abnormalities. Conversely, drawing supported and non-tracing may be most specific, given higher inherent consistency.
We also simulated abnormal spirals that vary in severity and were designed to simulated tremulous oscillations. As expected, these abnormal spirals were distinguishable from the drawn spirals of healthy volunteers (Figure 5B,5C). Non-tremulous disorders of motor control (e.g., bradykinesia) may not be as readily captured by this system. Future work will look to adequately simulate these conditions, in order to improve their identification using this application.
We also observed that the choice of stylus or finger did affect the consistency of spiral metrics. As a result, we caution users to interpret results according to the drawing implement used. Further, as with the instruction sets discussed above, we note that use of stylus could provide more precise and specific results, and that using a finger could provide more sensitive results.
Implementing this application as a web-based platform provides great flexibility. Users need not download the application. They can instead navigate to a website on any WiFi-enabled touchscreen device. Given the recent expansion of teleneurology, this and similar applications may support the push to integrate smartphones and sensors to capture high quality, remote and objective data (26).
Potential limitations include the varying technical characteristics of accessing devices. Prior studies employed Wacom tablets, which record drawing pressure and provide unparalleled accuracy in stylus position. There may be inherent differences in the sensitivity of Mac or Android devices to stylus drawing or finger drawing. Because technical specifications are not public, we are unable to comment on device differences, but instead note this limitation and urge users to interpret their results with caution when moving between devices. Additionally, our application is limited by design to only capture coordinates in the 2D plane. Wacom applications capture pressure and Z-axis deviations, but this capacity is limited as increasing tremor severity causes users to lift their styli. Future work will determine how well our application handles such situations. Future experiments will also establish how well this application identifies abnormal movements in specific diverse patient populations, for example, in parsing those with tremor due to dystonia from those with tremor due to ET. We will also seek to understand how spiral drawing performance changes with normal aging and with disease progression, with an eye to how the application can inform clinicians about subtle differences in performance in order to better inform treatment recommendations as normal aging and disease progression exacerbate symptoms. However, our application confers benefit over prior Wacom applications in being widely accessible from any WiFi-connected, mobile touchscreen device.
Acknowledgments
Funding: All authors were supported by Thomas Jefferson University institutional funds. Publication made possible in part by support from the Thomas Jefferson University Open Access Fund.
Footnote
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at https://dx.doi.org/10.21037/mhealth-21-16
Peer Review File: Available at https://dx.doi.org/10.21037/mhealth-21-16
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/mhealth-21-16). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was exempted by the Thomas Jefferson University Institutional Review Board (Control #20E.990) and informed consent was taken from all individual participants.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Schuhmayer N, Weber C, Kieler M, et al. Task-dependent variability of Essential Tremor. Parkinsonism Relat Disord 2017;41:79-85. [Crossref] [PubMed]
- Haubenberger D, Kalowitz D, Nahab FB, et al. Validation of digital spiral analysis as outcome parameter for clinical trials in essential tremor. Mov Disord 2011;26:2073-80. [Crossref] [PubMed]
- Lin PC, Chen KH, Yang BS, et al. A digital assessment system for evaluating kinetic tremor in essential tremor and Parkinson's disease. BMC Neurol 2018;18:25. [Crossref] [PubMed]
- Solé-Casals J, Anchustegui-Echearte I, Marti-Puig P, et al. Discrete Cosine Transform for the Analysis of Essential Tremor. Front Physiol 2019;9:1947. [Crossref] [PubMed]
- Louis ED, Yu Q, Floyd AG, et al. Axis is a feature of handwritten spirals in essential tremor. Mov Disord 2006;21:1294-5. [Crossref] [PubMed]
- Wang S, Bain PG, Aziz TZ, et al. The direction of oscillation in spiral drawings can be used to differentiate distal and proximal arm tremor. Neurosci Lett 2005;384:188-92. [Crossref] [PubMed]
- Louis ED, Gillman A, Boschung S, et al. High width variability during spiral drawing: further evidence of cerebellar dysfunction in essential tremor. Cerebellum 2012;11:872-9. [Crossref] [PubMed]
- Hsu AW, Piboolnurak PA, Floyd AG, et al. Spiral analysis in Niemann-Pick disease type C. Mov Disord 2009;24:1984-90. [Crossref] [PubMed]
- San Luciano M, Wang C, Ortega RA, et al. Digitized Spiral Drawing: A Possible Biomarker for Early Parkinson's Disease. PLoS One 2016;11:e0162799. [Crossref] [PubMed]
- Hess CW, Hsu AW, Yu Q, et al. Increased variability in spiral drawing in patients with functional (psychogenic) tremor. Hum Mov Sci 2014;38:15-22. [Crossref] [PubMed]
- Longstaff MG, Heath RA. Spiral drawing performance as an indicator of fine motor function in people with multiple sclerosis. Hum Mov Sci 2006;25:474-91. [Crossref] [PubMed]
- DelMastro HM, Ruiz JA, Gromisch ES, et al. Quantification characteristics of digital spiral analysis for understanding the relationship among tremor and clinical measures in persons with multiple sclerosis. J Neurosci Methods 2018;307:254-9. [Crossref] [PubMed]
- Miralles F, Tarongí S, Espino A. Quantification of the drawing of an Archimedes spiral through the analysis of its digitized picture. J Neurosci Methods 2006;152:18-31. [Crossref] [PubMed]
- Kraus PH, Hoffmann A. Spiralometry: computerized assessment of tremor amplitude on the basis of spiral drawing. Mov Disord 2010;25:2164-70. [Crossref] [PubMed]
- Miralles F, Tarongí S, Espino A. Quantitative evaluation of the drawing of a spiral on a paper. Mov Disord 2011;26:1369-author reply 1369-70. [Crossref] [PubMed]
- Saunders-Pullman R, Derby C, Stanley K, et al. Validity of spiral analysis in early Parkinson's disease. Mov Disord 2008;23:531-7. [Crossref] [PubMed]
- Wang H, Yu Q, Kurtis MM, et al. Spiral analysis-improved clinical utility with center detection. J Neurosci Methods 2008;171:264-70. [Crossref] [PubMed]
- Elble RJ, Ellenbogen A. Digitizing Tablet and Fahn-Tolosa-Marín Ratings of Archimedes Spirals have Comparable Minimum Detectable Change in Essential Tremor. Tremor Other Hyperkinet Mov (N Y) 2017;7:481. [Crossref] [PubMed]
- Westin J, Dougherty M, Nyholm D, et al. A home environment test battery for status assessment in patients with advanced Parkinson's disease. Comput Methods Programs Biomed 2010;98:27-35. [Crossref] [PubMed]
- Westin J, Ghiamati S, Memedi M, et al. A new computer method for assessing drawing impairment in Parkinson's disease. J Neurosci Methods 2010;190:143-8. [Crossref] [PubMed]
- Westin J, Schiavella M, Memedi M, et al. Validation of a home environment test battery for supporting assessments in advanced Parkinson's disease. Neurol Sci 2012;33:831-8. [Crossref] [PubMed]
- Sisti JA, Christophe B, Seville AR, et al. Computerized spiral analysis using the iPad. J Neurosci Methods 2017;275:50-4. [Crossref] [PubMed]
- Ishii N, Mochizuki Y, Shiomi K, et al. Spiral drawing: Quantitative analysis and artificial-intelligence-based diagnosis using a smartphone. J Neurol Sci 2020;411:116723. [Crossref] [PubMed]
- Ondo WG, Wang A, Thomas M, et al. Evaluating factors that can influence spirography ratings in patients with essential tremor. Parkinsonism Relat Disord 2005;11:45-8. [Crossref] [PubMed]
- Pullman SL. Spiral analysis: a new technique for measuring tremor with a digitizing tablet. Mov Disord 1998;13:85-9. [Crossref] [PubMed]
- Dorsey ER, Glidden AM, Holloway MR, et al. Teleneurology and mobile technologies: the future of neurological care. Nat Rev Neurol 2018;14:285-97. [Crossref] [PubMed]
Cite this article as: Magee R, Yang B, Ratliff J. Trsper: a web-based application for Archimedes spiral analysis. mHealth 2022;8:3.


